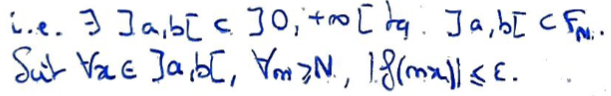Démonstration du théorème de Baire :

On construit une suite de fermés emboîtés en prenant un point arbitraire dans chaque ouvert et une boule autour de ce point.

On peut forcer le diamètre à tendre vers \(0\) en bornant le rayon des boules.

On utilise le Lemme des fermés emboîtés, qui nous donne la densité dans \(U_0\) puisque le point de départ et le rayon de départ sont arbitraires.

On conclut par densité de \(U_0\).

Preuve du théorème de Baire pour les fermés :

Il suffit d'appliquer le théorème de Baire et de passer au complémentaire

Montrer qu'un espace vectoriel normé admettant une base dénombrable n'est pas complet.

Pour \(n\) donné, on pose le sous-espace vectoriel engendré par les \(n\) premiers vecteurs de la base \(\to\) c'est un fermé.

On montre qu'ils sont d'intérieur vide en disant qu'aucun \(F_n\) ne contient une boule.

Puisque leur union est \(E\), on peut conclure via le Théorème de Baire.

Soit une application continue \(f:]0,+\infty[\to{\Bbb R}\) telle que $$\forall x\gt 0,\quad \underset{n\to+\infty}{\operatorname{lim} } f(nx)=0.$$
Montrer que \(\displaystyle\lim_{x\to+\infty}f(x)=0\).

On pose \(F_n\) l'ensemble des points \(x\) pour lesquels pour tout entier \(p\geqslant n\), \(\lvert f(px)\rvert\leqslant\varepsilon\).

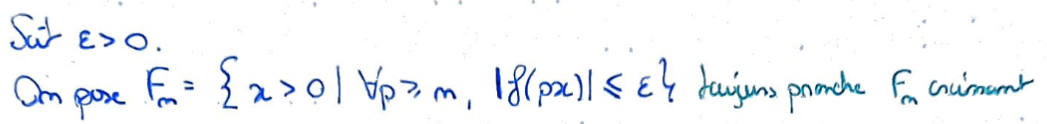
On peut écrire \(F_n\) comme une intersection dénombrable de fermés (via image réciproque par \(f\) continue), ce qui montre que \(F\) est fermé.

L'union des \(F_n\) est \(]0,+\infty[\), qui est de Baire (métrique complet), donc d'après le Théorème de Baire, il existe un \(F_n\) d'intérieur non vide.

Donc il existe un intervalle ouvert et \(N\) pour lesquels \(\forall n\geqslant N,\lvert f(nx)\rvert\leqslant\varepsilon\).